Python DeepLearningに再挑戦 8 ニューラルネットワークの学習 その2

概要

Python DeepLearningに再挑戦 8 ニューラルネットワークの学習 その2

参考書籍

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

ミニバッチ学習

機械学習の問題は、訓練データを使って学習する->訓練データに対する損失関数を求めて、その値をできるだけ小さくするように設定する　というのを繰り返すという作業。訓練データが１００個ある場合は、その100個の損失関数の和を指標とする。

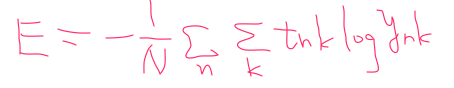
最後にNで割って正規化をしているところがポイントで、これをすることにより、1個あたりの平均の損失関数を求めることができる。

MNISTのように60,000個とか結構たくさんのデータがある時は全部の損失関数を計算するとめっちゃ時間がかかる。そのため、任意の枚数を選んで、ミニバッチとしてまとめて、ミニバッチごとに学習を行う。例えば、60000枚から無作為に１００枚選んで、その１００枚を使って学習をする。

多分、ミニバッチで、損失関数のスコアが良かったパラメータを使って元の６万枚とかを学習すると効率がいいとかそういうことなのかな。

ランダムにミニバッチを選ぶには以下のようにコードを書く。

train_size = x_train.shape[0] # x_trainデータ全体のshapeの[0]、つまり60,000。
batch_size = 10 # 取り出すバッチの数
batch_mask = np.random.choice(train_size, batch_size) # 60,000のなかから、10個を選ぶ
x_batch = x_train[batch_mask] # 選んだ10個の画像（の配列）をゲットする。
t_batch = t_train[batch_mask] # 選んだ10個のラベル（の配列）をゲットする。

試しに、np.random.choice(60000, 10) とかうつとランダムで10個取り出される。

バッチ対応版　交差エントロピー誤差の実装

# yはニューラルネットワークの出力、tは教師データ
# こちらは、one-hot 表現の場合（正解だけが、1でそれ以外は、0）
def cross_entropy_error(y, t):
    if y.ndim == 1: # １次元の場合、つまりデータの次元が７８４の配列１つである場合
        t = t.reshape(1, t.size) # reshapeで、１次元に変換するのかな。sizeは配列の要素数。
        y = y.reshape(1, y.size) 
    
    batch_size = y.shape[0] # 平たくいうと、出力データ数。
    return -np.sum(t * np.log(y)) / batch_size # 交差エントロピーの合計をバッチサイズで割り算する。


# こちらはone-hotではなく、0,1,2,3などラベル名としてtが与えられた場合
def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
# ここまでは一緒
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size

ポイント： * np.arange(batch_size)は、0~batch_size -1 までの配列を作成する。例えば、batch_sizeが１０の場合は、[0,1,...8]までを作成する。 * tにはラベルが、[2,5,4,6,9 ....1] のように格納されている。 * そのため、y[np.arange(batch_size),t ] は、y[[0....9],[2,4,3,3,2....]]という形になる。 * 結果的に、[y[0,2], y[1,7], y[2, 0, ....] という形の配列を生成する。これは、各データの正解ラベルに対応するニューラルネットワークの出力を抽出している。

む〜〜〜、難しいw

損失関数の意味

• 認識精度ではなく、損失関数を指標とするのは、ニューラルネットワーク学習の時に使う「微分」と関係している。
• 最適な重みとバイアスを探す時に、損失関数の値ができるだけ小さくなるようなパラメータを探す。
• そのために、微分を計算して、その微分の値を手掛かりにパラメータの値を徐々に更新していく。
• 認識精度を指標にするとほとんどの場所で０になってしまい、パラメータの更新ができなくなるため。

次回から、数値微分か〜おもしろそうやなぁ(^ ^)